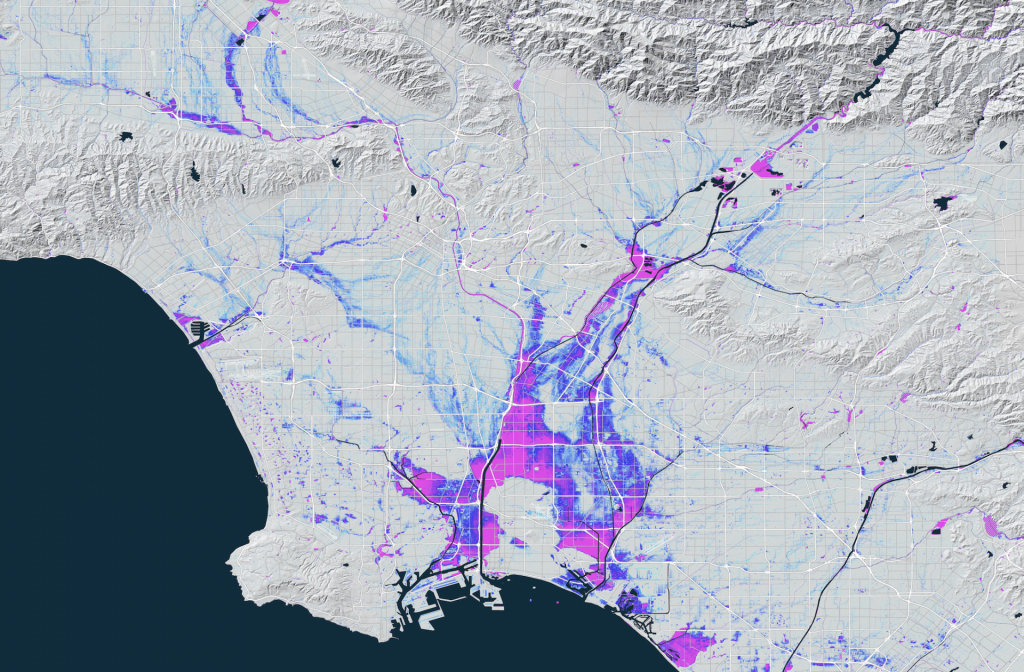
Flooding and erosion has emerged as one the greatest climate challenges facing the world. Losses are escalating at an alarming rate, and millions of people are impacted by flooding every year. At the UCI Flood Lab, we advance simulation technologies for characterizing flooding and erosion dynamics, and we join trans-disciplinary research teams and work with affected communities to integrate these technologies into actionable information and better policies for management.


We envision a future where advanced simulation technologies developed by engineers are more interactive and accessible to everyone, and more trusted, to contemplate the possibility of flooding and erosion, how people and the environment might be impacted, and what can be done about it.